Anagram Substring Search — Find all anagrams in a string
Given a string, find all anagrams of a pattern in the given string.
For example:
INPUT : string = “abczzbcabcadeb”, pattern = “abc”
OUTPUT: [0,5,6,7,8]An anagram is defined as a word which is formed by re-arranging letters of a given word. For example, the words LISTEN and SILENT are anagrams of each other. Therefore, when we have to find ALL anagrams of a pattern, it means all possible combinations of a pattern by rearranging the letters of a given word. Therefore, if we are given a pattern “abc”, then all of its anagrams will be
[“abc”, “acb”, “bac”, “bca”, “cab”, “cba”]
The goal of this problem is to find the all the indices, where any anagram of a given pattern is found in a string. The following diagram will make things a bit clearer:
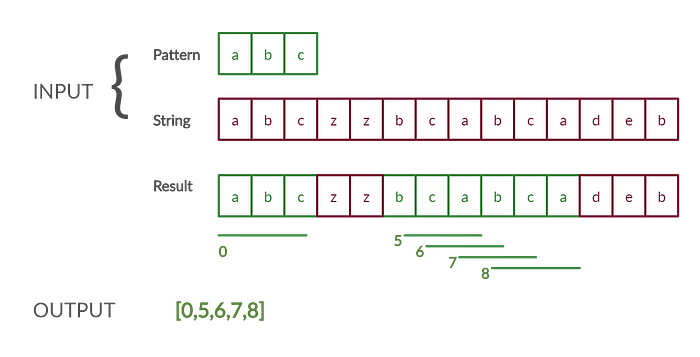
In the above diagram, at index 0, “abc” is found, then at index 5, “bca” is found, at index 6, “cab” is found, at index 7, “abc” is found and finally at index 8, “bca” is found. Therefore, the result becomes: [0,5,6,7,8]
Now that we’ve got our goal sorted, let’s understand how we can translate it into a program.
One way to do it is to find all the combinations of the pattern, and then run a loop through the string and try to check if each substring(from i to i+patternLength) is equal to any combination of the pattern.
However, the biggest problem with this approach is that the number of combinations of a string depends on the number of characters in the string. A pattern of length ‘m’, can have ‘m!’ combinations. As we saw above with the pattern “abc”, there are 3 characters with [3! = 3 * 2 * 1 = 6] combinations. If the pattern becomes larger, the combinations too, significantly increase.
When we run the loop from 0 to (stringLength-patternLength-1). In each iteration, we check for the equality of each substring with each combination. If string is of length ’n’, then the runtime complexity of this approach becomes:
O((n-m-1) * m!)
Now, n>m (stringLength > patternLength)
So we leave out the less dominant terms (-m & -1), we get:
O(n * m!)This runtime complexity is huge, and therefore non-pragmatic.
The bottleneck with the approach is the m! combinations that we have to iterate through. In order to optimize the runtime, we have to find a way to do this without calculating (and iterating through) all the combinations of the pattern.
Let’s analyze how we can do this:
Map-based Sliding Window Approach
In this approach, we take two “windows”,
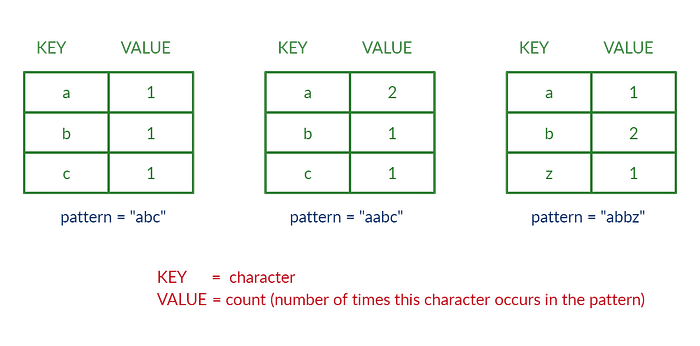
1We create a window for the pattern. In this window, we create a map of all the characters present in the pattern as keys and the number of times each character occurs in the window (counts) as values. The following diagram shows how your patternMap would look like for different patterns:
2Next, we create another window (substringMap) which is the size of the pattern. We compare this substring window (substringMap) with the pattern window (patternMap) and check whether the two windows have same characters with exact same count.
The reason we are using characters and their counts, is that the key-value pairs of a map for any string would be the same for any combination. For example,
Given the pattern: “abc”, the map {a=1, b=1, c=1}, will be same for any combination of “abc” i.e [“abc”, “acb”, “bac”, “bca”, “cab”, “cba”]. Therefore, it removes the biggest bottleneck of finding and iterating through combinations.
In the given example of the string abczzbcabcadeb, let’s see how the windows of this string will look like while iterating through the string. Please note that the pattern window will always be the same.
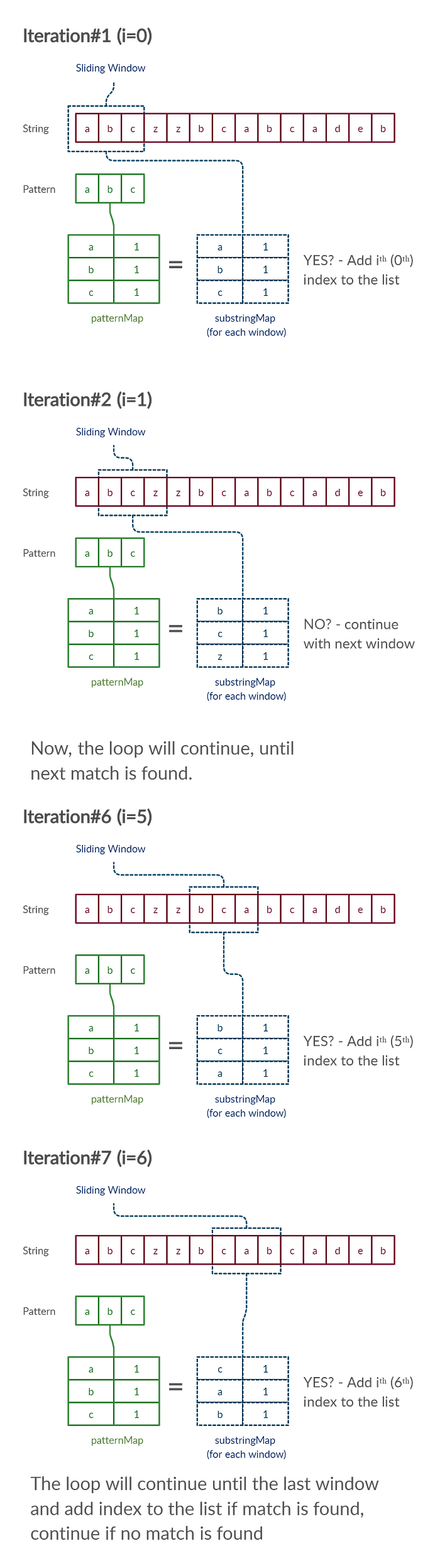
Now that we’ve got the visualization of this algorithm, let’s transform this into an actual program.
List<Integer> findAnagramsOfPatternInString(String string, String pattern) {
if(isEmpty(string) || isEmpty(pattern)){
System.out.println("Invalid string or pattern");
return null;
}
if(pattern.length() > string.length()) {
System.out.println("Pattern is larger than the string");
return null;
}
Map<Character, Integer> patternMap= new HashMap<>();
Map<Character, Integer> substringMap = new HashMap<>();
List<Integer> foundIndices = new ArrayList<>();
//we create two windows - one for pattern and other for the
//first substring
for(int i=0; i<pattern.length(); i++) {
addCharToWindow(pattern.charAt(i), patternMap);
addCharToWindow(string.charAt(i), substringMap);
}
//start at the end of the first window
for(int windowRightBound = pattern.length(); windowRightBound < string.length(); windowRightBound++) {
if(compare(patternMap, substringMap)) {
//add to list if maps are equal
foundIndices.add(windowRightBound - pattern.length());
}
//1. Remove the first character in the window
int windowBegin_oldIndex = (windowRightBound -
pattern.length());
Character staleCharacter =
string.charAt(windowBegin_oldIndex);
Integer staleCharacterCount =
substringMap.get(staleCharacter);
if(staleCharacterCount == 1) {
substringMap.remove(staleCharacter);
} else {
staleCharacterCount--;
substringMap.put(staleCharacter, staleCharacterCount);
}
//2. Add the new character in the window
addCharToWindow(string.charAt(windowRightBound),
substringMap);
}
//at this point, the last comparison window still remains,
//so we still compare one last time
if(compare(patternMap, substringMap)) {
foundIndices.add(string.length() - pattern.length());
}
return foundIndices;
}//method which returns true if a string is empty
boolean isEmpty(String string) {
return string == null || pattern == null ||
string.length() == 0 || pattern.length() == 0;
}//adds a character to the window. The window map is the argument
void addCharToWindow(Character character, Map<Character, Integer> map) {
Integer count = map.get(character);
if(count == null) {
count = 0;
}
count++;
map.put(character, count);
}//compare maps
boolean compare(Map<Character, Integer> patternMap, Map<Character, Integer> substringMap) {
for(Map.Entry<Character, Integer> eachEntry:
patternCounts.entrySet()) {
Character eachCharacter = eachEntry.getKey();
Integer eachCount = eachEntry.getValue();
if(substringMap.get(eachCharacter) == null ||
substringMap.get(eachCharacter) != eachCount) {
return false;
}
}
return true;
}
Now, let’s analyze the runtime complexity of this solution. Considering ‘m’ as the size of the pattern and ’n’ the size of the string.
First, we create the maps of pattern and first substring (size m)
i.e. O(m) complexityNext, we iterate through the string of size 'n'
i.e. O(n) complexity=> O(m+n)complexity.
Here, m < n; so we leave out the less dominant term (i.e. m)=> O(n) runtime complexity
A question may arise, that in each iteration through string, we are comparing two maps, which have their own loops. Why is that complexity not considered?
The answer is simple: The characters present in the string will always come from a unique set of characters. For example, if this problem comes with a constraint that the string can contain English alphanumeric characters, then the number of unique characters will be:
a-z | 26 characters
A-Z | 26 characters
0-9 | 10 characters
i.e. total of 26 + 26 + 10 = 62 charactersTherefore, the compare() method will have at most 62 characters to compare, which is a constant number. And if we are looping (for comparison) upto a constant iterations (i.e. 62 in this case), the runtime complexity of comparison will be in O(1) time (or constant time). Therefore, the comparison can be considered a constant time operation and the final runtime complexity will be as calculated: O(n): where n is the length of the string.
Questions? Comments? Please feel free to write through the comments : )
